POJ 1191棋盘分割 - zero91's Blog
POJ 1191棋盘分割
zero91
posted @ Sat, 14 May 2011 23:45:39 +0800
in 解题报告
, 1069 readers
原题目如下(http://poj.org/problem?id=1191):
Description
将一个8*8的棋盘进行如下分割:将原棋盘割下一块矩形棋盘并使剩下部分也是矩形,再将剩下的部分继续如此分割,这样割了(n-1)次后,连同最后剩下的矩形棋盘共有n块矩形棋盘。(每次切割都只能沿着棋盘格子的边进行)

原棋盘上每一格有一个分值,一块矩形棋盘的总分为其所含各格分值之和。现在需要把棋盘按上述规则分割成n块矩形棋盘,并使各矩形棋盘总分的均方差最小。
均方差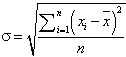

 ,其中平均值
,其中平均值 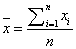 ,xi为第i块矩形棋盘的总分。
,xi为第i块矩形棋盘的总分。
请编程对给出的棋盘及n,求出O'的最小值。

原棋盘上每一格有一个分值,一块矩形棋盘的总分为其所含各格分值之和。现在需要把棋盘按上述规则分割成n块矩形棋盘,并使各矩形棋盘总分的均方差最小。
均方差
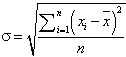

 ,其中平均值
,其中平均值 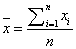 ,xi为第i块矩形棋盘的总分。
,xi为第i块矩形棋盘的总分。请编程对给出的棋盘及n,求出O'的最小值。
Input
第1行为一个整数n(1 < n < 15)。
第2行至第9行每行为8个小于100的非负整数,表示棋盘上相应格子的分值。每行相邻两数之间用一个空格分隔。
第2行至第9行每行为8个小于100的非负整数,表示棋盘上相应格子的分值。每行相邻两数之间用一个空格分隔。
Output
仅一个数,为O'(四舍五入精确到小数点后三位)。
Sample Input
3 1 1 1 1 1 1 1 3 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 0 3
Sample Output
1.633
Source
分析:题目要求分割成n份之后,均方差最小。而平均值是已知的,故由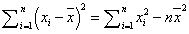 得,只需要求出
得,只需要求出 的最小值即可,而
的最小值即可,而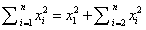 ,不难得出如果
,不难得出如果 最小,一定会有
最小,一定会有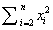 最小,也就是说问题具有最优子结构的性质,这让我们想到了DP。题目要求在切割矩形的时候,每一次分出的一定是两个矩形,且切割矩形的时候,有两个方向可以切,横切和竖切,横切和竖切分别可以有两个不同的子问题,只需要求出这些子问题中满足题目要求的最优值即可。另外,我们需要存储当前的子问题是处于哪个子矩阵范围内,这就必然需要存储矩阵信息,最自然的就是想到用数组的下标来存储,所以,这一题可以使用数组的四维来表示一个完整的子矩阵。由以上可以知道,解决此问题就相当于求解有n个子矩阵时的最优值,而当只有1个子矩阵时,也就是该矩阵本身,这个可以直接从输入信息中得出,做一个预处理即可。采用自下向上程序实现方法就可以了。
最小,也就是说问题具有最优子结构的性质,这让我们想到了DP。题目要求在切割矩形的时候,每一次分出的一定是两个矩形,且切割矩形的时候,有两个方向可以切,横切和竖切,横切和竖切分别可以有两个不同的子问题,只需要求出这些子问题中满足题目要求的最优值即可。另外,我们需要存储当前的子问题是处于哪个子矩阵范围内,这就必然需要存储矩阵信息,最自然的就是想到用数组的下标来存储,所以,这一题可以使用数组的四维来表示一个完整的子矩阵。由以上可以知道,解决此问题就相当于求解有n个子矩阵时的最优值,而当只有1个子矩阵时,也就是该矩阵本身,这个可以直接从输入信息中得出,做一个预处理即可。采用自下向上程序实现方法就可以了。
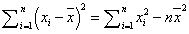 得,只需要求出
得,只需要求出 的最小值即可,而
的最小值即可,而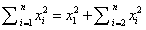 ,不难得出如果
,不难得出如果 最小,一定会有
最小,一定会有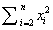 最小,也就是说问题具有最优子结构的性质,这让我们想到了DP。题目要求在切割矩形的时候,每一次分出的一定是两个矩形,且切割矩形的时候,有两个方向可以切,横切和竖切,横切和竖切分别可以有两个不同的子问题,只需要求出这些子问题中满足题目要求的最优值即可。另外,我们需要存储当前的子问题是处于哪个子矩阵范围内,这就必然需要存储矩阵信息,最自然的就是想到用数组的下标来存储,所以,这一题可以使用数组的四维来表示一个完整的子矩阵。由以上可以知道,解决此问题就相当于求解有n个子矩阵时的最优值,而当只有1个子矩阵时,也就是该矩阵本身,这个可以直接从输入信息中得出,做一个预处理即可。采用自下向上程序实现方法就可以了。
最小,也就是说问题具有最优子结构的性质,这让我们想到了DP。题目要求在切割矩形的时候,每一次分出的一定是两个矩形,且切割矩形的时候,有两个方向可以切,横切和竖切,横切和竖切分别可以有两个不同的子问题,只需要求出这些子问题中满足题目要求的最优值即可。另外,我们需要存储当前的子问题是处于哪个子矩阵范围内,这就必然需要存储矩阵信息,最自然的就是想到用数组的下标来存储,所以,这一题可以使用数组的四维来表示一个完整的子矩阵。由以上可以知道,解决此问题就相当于求解有n个子矩阵时的最优值,而当只有1个子矩阵时,也就是该矩阵本身,这个可以直接从输入信息中得出,做一个预处理即可。采用自下向上程序实现方法就可以了。
#include <stdio.h>
#include <math.h>
#define MAX_N 8
#define MAX 15
#define INF 999999999
#define minv(a,b) ( (a) < (b) ? (a) : (b) )
int pointV[ MAX_N+1 ][ MAX_N+1 ][ MAX_N+1 ][ MAX_N+1 ];
int dp[ MAX_N+1 ][ MAX_N+1 ][ MAX_N+1 ][ MAX_N+1 ][ MAX ];
void
init( int n )
{
int x1, y1, x2, y2, i;
for( x1 = 1; x1 <= MAX_N; ++x1 )
for( y1 = 1; y1 <= MAX_N; ++y1 )
for( x2 = x1; x2 <= MAX_N; ++x2 )
for( y2 = y1; y2 <= MAX_N; ++y2 ){
if( x1 != x2 || y1 != y2 ){
pointV[x1][y1][x2][y2] = pointV[x1][y1][x2-1][y2] +
pointV[x1][y1][x2][y2-1] - pointV[x1][y1][x2-1][y2-1] +
pointV[x2][y2][x2][y2];
}
dp[x1][y1][x2][y2][1] = pointV[x1][y1][x2][y2] * pointV[x1][y1][x2][y2];
for( i = 2; i <= n; ++i )
dp[x1][y1][x2][y2][i] = INF;
}
}
void
getResult( int n )
{
int k, x1, y1, x2, y2, i;
int temp;
for( k = 2; k <= n; ++k )
for( x1 = 1; x1 <= MAX_N; ++x1 )
for( y1 = 1; y1 <= MAX_N; ++y1 )
for( x2 = x1; x2 <= MAX_N; ++x2 )
for( y2 = y1; y2 <= MAX_N; ++y2 ){
for( i = x1; i < x2; ++i ){
temp = minv( dp[x1][y1][i][y2][k-1] + dp[i+1][y1][x2][y2][1],
dp[i+1][y1][x2][y2][k-1] + dp[x1][y1][i][y2][1] );
if( temp < dp[x1][y1][x2][y2][k] )
dp[x1][y1][x2][y2][k] = temp;
}
for( i = y1; i < y2; ++i ){
temp = minv( dp[x1][y1][x2][i][k-1] + dp[x1][i+1][x2][y2][1],
dp[x1][i+1][x2][y2][k-1] + dp[x1][y1][x2][i][1] );
if( temp < dp[x1][y1][x2][y2][k] )
dp[x1][y1][x2][y2][k] = temp;
}
}
}
int
main( void )
{
int n;
int i, j;
double average = 0.0;
scanf( "%d", &n );
for( i = 1; i <= MAX_N; ++i )
for( j = 1; j <= MAX_N; ++j ){
scanf( "%d", &pointV[i][j][i][j] );
average += pointV[i][j][i][j];
}
average /= n;
init( n );
getResult( n );
printf( "%.3f\n", sqrt( (double)dp[1][1][MAX_N][MAX_N][n]/n - average*average ) );
return 0;
}
 Comments (0)
Comments (0)